Gas Laws:
The macroscopic behavior of gases can be described by certain generalization. These generalized observations are called bas laws.
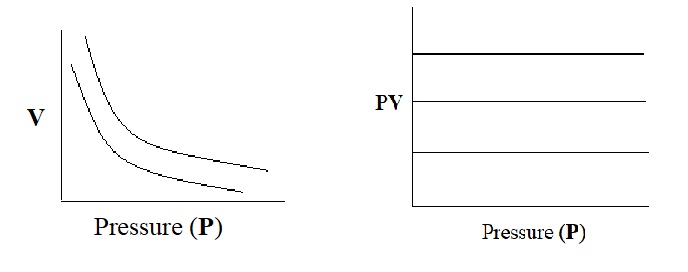
1) Boyle’s Law (Pressure-Volume Relationship):
According to Boyle’s law, at constant temperature, the volume of a given mass of a gas is inversely proportional to the pressure exerted on it. Therefore, Boyle’s law may be expressed as-
V α 1/P At constant temperature (T).
Or, V = K/P where K is a constant
Or, PV = K (constant).
Suppose a given mass of a gas has a volume V1 at pressure P1 at certain temperature T, then according to Boyle’s law,
P1V1 = K (at constant T) —– (i)
Suppose now the volume is changed to V2 and its pressure becomes P2 while temperature T is kept constant, then
P2V2 = K (at constant T) —– (ii)
From expression (i) and (ii) we get,
P1V1 = P2V2 = K (constant)
Thus Boyle’s law may also be state that “the product of volume of a given mass of the gas and its pressure is constant at constant temperature”.
Graphical representation of Boyle’s law:
Q: The volume of a gas is 50 cc when the pressure is 750 mm. what will be it volume when the pressure is increased to 770mm?- Q: A vessel of 120 ml capacity contains a certain mass of a gas at 20◦C and 750 mm pressure. The gas was transferred to vessel whose volume is 180 ml. Calculate the pressure of the gas at 20◦C.
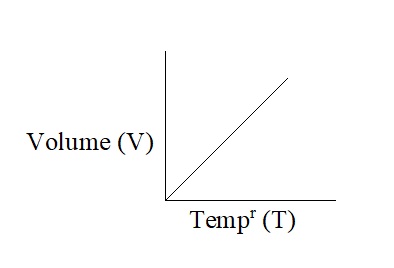
2) Charles’ Law:
According to Charles’ law “the volumes of a given mass of a gas increases or decreases by 1/273 of its volume at 0◦C for every one degree centigrade rise or fall in temperature”. Therefore,
V = (V0 + V0/273) t◦c
Where, V = volume of the gas at t◦c.
V0 = volume of the gas at 0◦c.
V = V0 (1+ t◦c/273)
V = V0 (273+ t◦c) /273
V = V0 (T/273)
V = (V0/273)/T
V/T = K (constant), Where, K = (V0/273)
T = Absolute temperature.
V α T, at constant pressure (P)
Thus, Charles’ law may also be state as- “The volume of a given mass of a gas is directly proportional to its absolute temperature at constant pressure”. Therefore,
Or, V α T, at constant pressure (P)
Or, V = K T, Where K is a constant
Or, V/T = K (constant)
If V1 and V2 be the volume at T1 and T2, then Charles’ law becomes,
V1/T1 = V2/T2 = ——— = K (constant)
Graphical Representation of Charles’ law:
Note:
The volume of the given gas should reduce to zero at -273◦C i.e. the gas disappears altogether. But it has been found that it never happens and before this condition is reached, the gases get liquefied.
This minimum imaginary temperature of -273◦C at which the volume of any gas tends to be zero is called the absolute zero temperature. The centigrade temperature (t) and the absolute or Kelvin temperature (T) are related as-
T = (t + 273) K
Question-1: 200cc of nitrogen at 27◦C are cooled to -20◦C. Find the new volume of the gas at the same pressure.
3) Avogadro’s Law:
According to Avogadro’s law, under similar condition of temperature and pressure equal volume of all gases contain equal number of molecules. E.g. 22.4 litres of any gas at NTP contain 6.023 X 10 23 molecules irrespective of its nature. Then, from Avogadro’s law, we have
V α n, At constant temperature (T) and pressure (P)
Where, n = No. of moles.
V = Volume of the gas.
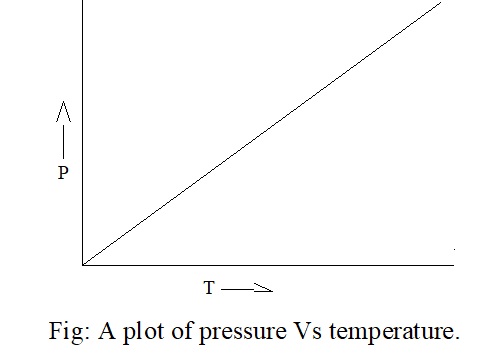
4) Gay Lussac’s Law (pressure-temperature relationship):
The relationship between pressure and temperature was given by Joseph Gay Lussac and is known as Gay Lussac law. According to this law, “at constant volume, the pressure of a fixed amount of gas varies directly with temperature”. Therefore,
P α T, at constant volume (V)
Or, P = K T where K is a constant
P1/T1 = P2/T2 = K (constant)
5) Derive Ideal Gas Equation:
The gases obeying the Boyles and Charles law is termed as ideal gas. A mathematical expression describing the simultaneous effect of the changes in temperature and pressure on the volume of a given amount of a gas is called ideal gas equation.
From Boyles law, we have
V α 1/P At constant temperature
From Charles law, we have
V α T, At constant pressure (P)
From Avogadro’s law, we have
V α n, At constant temperature (T) and pressure (P)
Combining Boyles, Charles and Avogadro’s law, we have
V α nT/P, when P, T, n vary
Or, V = KnT/P Where K is a constant.
Or, PV = nKT
Now changing the constant K into R (Universal gas constant) then the above expression becomes-
PV = nRT ——– (1)
The expression (1) is for n mole of gas, then for one mole of gas the expression (1) becomes,
PV = RT ——- (2)
6) Universal gas constant (R):
In order to understand the significance of R, let us examine the nature of quantities in the ideal gas equation.
PV = nRT
Or, R = PV/nT
Or, R = (Pressure x Volume)/ (no. of moles x Abs. temperature)
Or, R = [force/ (length) 2 x (length) 3/ (no. of moles x Abs. temperature)]
Or, R = (force x length)/ (no. of moles x Abs. temperature)
Or, R = work/ (no. of moles x Abs. temperature)
Thus, the universal gas constant is a measure of energy (work done) per mole of the gas for one degree change in its temperature. Therefore,
R = PV/nT
Or, R = (1 x 22.4) atm. litre / (1 x 273) mole. Kelvin.
Or, R = 0.0821 Litre. atm K-1mol-1
Question:
- At 27◦C a gas under a pressure of 750 mm occupies a volume of 73 ml. Calculate the volume of the gas at NTP.
- The volume of a certain quantity of oxygen is 260 cc when the temperature is 15◦C and pressure is 740 mm. what would be the temperature so that the volume becomes 180 cc under 750mm pressure?
- Calculate the mass of 120 ml of nitrogen at 150◦C and 1 atmosphere pressure.
7) Kinetic Molecular Theory:
The important postulates of kinetic molecular theory are-
1) All gases are made up of a very large number of minute particles (atoms or molecules).
2) The molecules are separated from one another by large distances. The empty spaces among the molecules are so large that the actual volume of the molecules is negligible as compared to the total volume of the gas.
3) The molecules are in a state of ceaseless and random motion in all the directions. During their motion, they keep on colliding with one another and also with the walls of the container and thus, change their directions.
4) Molecular collisions are perfectly elastic, i.e. no loss of energy occurs when the molecules collide with one another or with the walls of the container.
5) There are no forces of interaction (attractive or repulsive) between molecules at ordinary temperature and pressure. They move completely independent of one another.
6) The pressure exerted by the gas is due to the collision of its molecules on the walls of the container per unit area.
7) The average kinetic energy of the gas molecules is directly proportional to the absolute temperature.
8) Kinetic Gas Equation:
On the basis of postulates of kinetic molecular theory, an equation was derived for the pressure of the gas. The equation is known as kinetic gas equation as-
PV = 1/3 mnv2
Where, V = Volume of the gas
m = mass of the molecules.
n = No. of molecules in the volume V.
v2 = root mean square velocity.
Deviation from ideal behavior:
A gas which obeys ideal gas equation (PV = nRT) and other gas laws at all temperatures and pressures is called an ideal gas or perfect gas. However, actually none of the known gases obey PV=nRT over the entire range of temperatures and pressures. At best, the gases show ideal behaviour at low pressures and high temperatures. As the pressure becomes high and temperature becomes low, more and more deviations are observed from ideal gas equation and other gas laws.
Deviations of Real Gases:
The gas which does not obey general gas equation and ether gas laws at all temperatures and pressures is called non-ideal gas or real gas.
All gases which are actually known to exist such as oxygen, nitrogen, carbon dioxide, etc. are real gases and they show ideal behaviour to different extents. Most of them show ideal behaviour at low pressures and high temperatures. Amagat Andrews and other scientists made extensive study of the behaviour of various gases under different conditions of temperatures and pressures. They concluded that real gases do not obey the PV = nRT under all conditions of temperature and pressure.
To test the behaviour of real gases, we plot PV versus P plot of gases at constant temperature. According to Boyle’s law, PV will be constant and PV versus P plots at all pressures will be straight line parallel to x-axis (fig: 1).
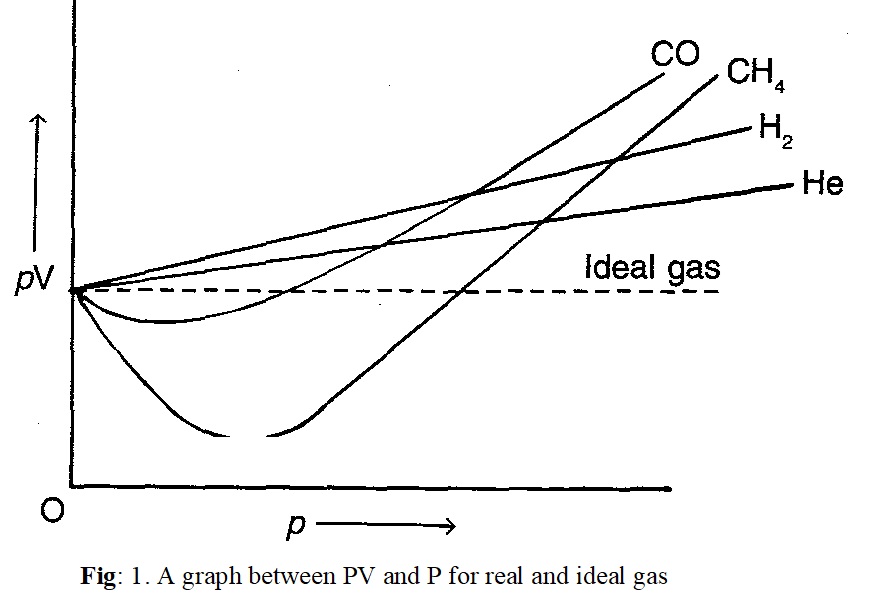
It can be seen easily from figure that at constant temperature PV versus P plot for real gases is not a straight line. There are significant deviations from ideal behaviour. Two types of curves are observed-
i) For gases such as hydrogen (H2) and helium (He) as the pressure increases the value of PV also increases.
ii) For gases such as carbon monoxide (CO) and methane (CH4) first there is a negative deviation from ideal behaviour so that PV decreases with increase in pressure. It reaches to a minimum value characteristic of a gas. After that PV value starts increasing. The curve crosses the line for ideal gas and after that shows positive deviation continuously.
Thus, real gases do not follow ideal gas equation perfectly at all conditions. Deviations from ideal behaviour also become clear when pressure versus volume plots are drawn. The pressure vs volume plot of experimental data (real gases) and that theoretically calculated from Boyle’s law (for ideal gas) should coincide if all gases behave ideally. This is shown in Fig.2. It is clear that they do not coincide. At high pressures the measured volume is more than the calculated volume. However, at low pressures measured and calculated volumes almost approach each other.
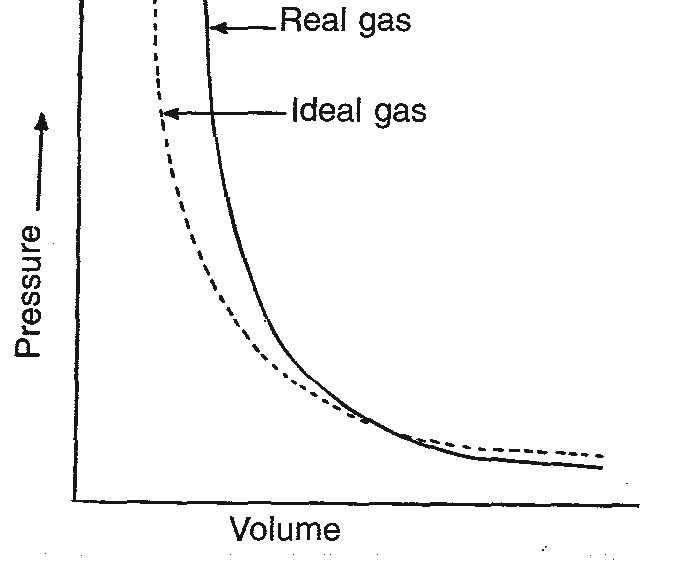Fig: 2. Plot of P against V for ideal and real gases.
Effect of pressure:
A study deviation of real gases from ideal behaviour is to plot a graph between (PV/nRT) and P. The quantity PV/nRT is called compressibility factor and is denoted by ‘Z’. Therefore,
Compressibility factor, Z = PV/nRT
For ideal gases, Z = 1 under all condition of temperature and pressure. Hence, PV is always equal to nRT and this corresponds to ideal behaviour.
For real gases, Z may be less than 1 or more than 1. Thus,
PV ≠ nRT
The (PV/nRT) versus P plots for some common gases such as H2, N2, O2, He, CH4 and CO2 are shown in Fig. 3.
It is clear from the figure that Z has values greater than and less than one (ideal behaviour).
(i) If Z < 1, it is called negative deviation. It means that the gas is more compressible than expected from ideal behaviour. e.g. N2, O2, CH4 and CO2.
(ii) If Z> 1, it is called positive deviation. It means that the gas is less compressible than expected from ideal behaviour. e.g. H2, He.
It is observed that the deviations are low at low pressure. This means that the equation PV = nRT (ideal gas equation) is almost valid at low pressures for all gases.
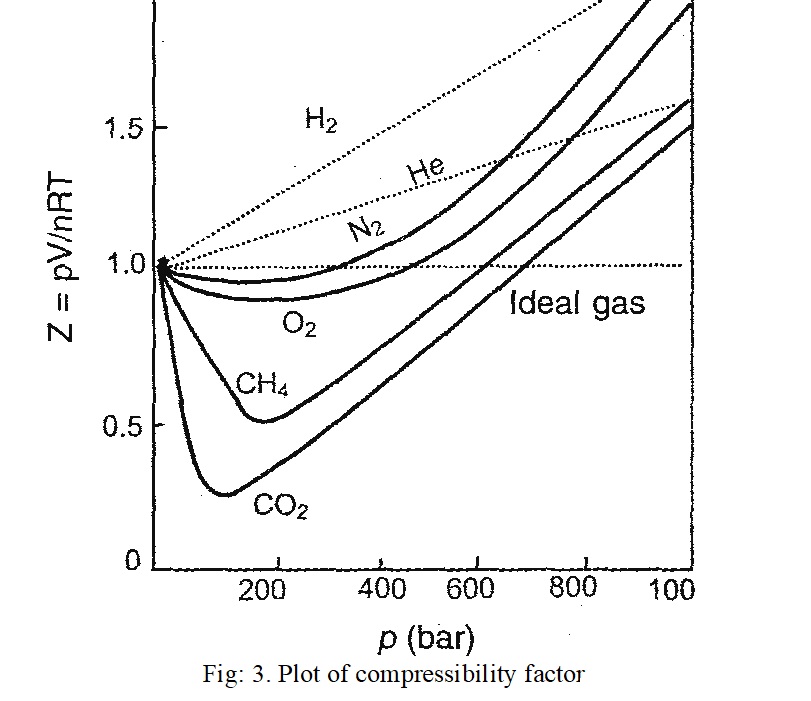At high pressures, Z is always greater than unity. The extent of deviation at any pressure or temperature depends upon the nature of the gas. Moreover, Z approaches unity as pressure approaches zero.
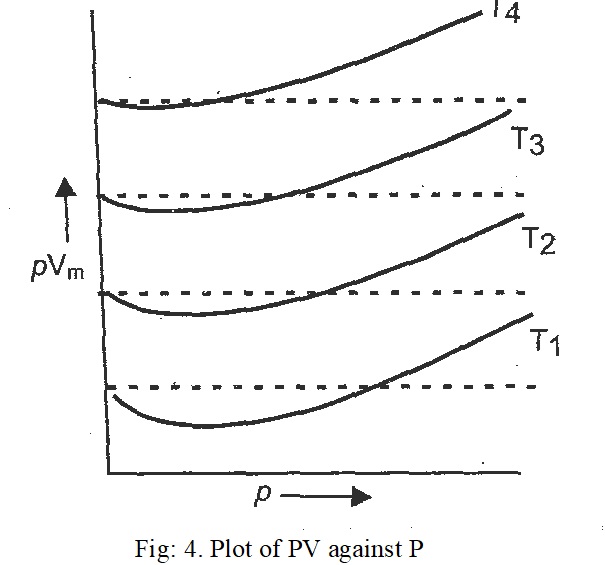
Effect of temperature:
The effect of temperature on the behaviour of real gases can be seen by comparing the behaviour of N2 gas at different temperatures. The value of PV at different temperatures is shown in Fig. 4. In this plot, the dotted lines represent ideal behaviour at that temperature. It is clear from the figure that dips in the curves goes on becoming smaller and smaller as the temperature increases. This means that the deviations from ideal behaviour become less and less with increase in temperature. At a certain temperature, the minimum in the curve vanishes and the curve remains horizontal for an appreciable range of pressure (ideal behaviour).
Note:
- At best the real gases show ideal behaviour at low pressures and fairly high temperatures
- At low temperatures and high pressures, the gases differ significantly from ideal behaviour.
Causes of Deviations from Ideal Behaviour:
In order to explain the deviations from ideality, van der Waal pointed out that the following two assumptions in kinetic theory are faulty. These are:
i) The molecules were considered as point masses and the volume occupied by the gas molecules is negligible in comparison to the total volume of the gas.
ii) It was assumed that there are no inter- molecular forces between and the molecules moved independently.
Corrections of Deviations — Van der Waals’ equation for Real Gases:-
To explain the behaviour of real gases, it becomes necessary to apply suitable corrections to the ideal gas equation, PV = nRT, so as to make it applicable to real gases. The ideal gas equation was modified by Van der Waals, who incorporated the idea of finite molecular volume and intermolecular forces. The modified equation of state which explains the deviations of real gases from ideality is known as Van der Waals’ equation of state. Van der Waals applied the corrections to the volume and pressure of the ideal gas equation.
i) Correction of volume: – The volume occupied by the molecules cannot be neglected in comparison to the total volume. It means that the molecules are not free to move in whole of volume V but the free volume is less than the observed volume. In other words, the ideal volume of a gas is less than observed volume. Therefore, a suitable correction term may be subtracted from the observed volume. The correction term for one mole of gas is ‘b’, which is a constant depends upon the nature of the gas and known as excluded volume. Thus,
V corrected = (V- b) for one mole of gas.
V corrected = (V- nb) for n mole of gas.
ii) Correction of Pressure: – Some attractive forces exist between the molecules of the real gases. Consider a molecule of a gas in the middle of the container (Fig. 5). The molecule is being attracted uniformly by the neighbouring molecules. The attractive forces neutralise one another and there is no resultant pull on the molecule.
On the other hand, when a molecule approaches the wall of the container, it experiences an inward pull as a result of the attractive forces exerted by the neighbouring molecules inside the vessel. Thus, the molecule strikes the wall with a lesser force than it would have done if there were no attractive forces. Therefore, the observed pressure is less than the ideal pressure. Consequently, some correction term should be added to the observed pressure in order to calculate ideal pressure. Hence, corrected pressure is given by-
P corrected = P + p, Where P is the observed pressure and p is the corrected term.
Van der Waals suggested that to correct the pressure, the pressure term p is equal to a/V2 for one mole and an2/V2 for n moles where ‘a’ is a constant which depends upon the nature of the gas. Thus,
P corrected = P + a/V2 for one mole of gas
P corrected = P + an2/V2 for n mole of gas
Substituting the corrected values of volume and pressure in ideal gas equation, PV = nRT, we get,
(P + an2/V2) (V-nb) = nRT for n mole of gas.
(P + a/V2) (V-b) = nRT for 1 mole of gas.
These equations are called Van der Waals’ equation of state.
Significance and units of a and b:
The constants a and b are called Van der Waals’ constants and their values depend upon the nature of the gas. The constant ‘a’ measures the forces of attraction between the molecules of a gas. Greater the value of ‘a’ greater is the strength of van der Waals interactions. It may be noted that the greater value of ‘a’ of a gas also reflects its greater tendency to be liquefied.
The constant ‘b’ relates to incompressible volume of the molecules and measures the effective size of gas molecules. It may be noted that ‘b’ is not equal to actual volume of the molecule but it is four times the actual volume of molecules.
Question: 1. One mole of carbon dioxide occupies 1.5 litres at 25◦C. calculate the pressure exerted by the gas using van der Waals’ equation where a = 3.6 L2 atm mol-2 and b = 0.04 L mol-1.
Question: 2. Two mole of ammonia were found to occupy a volume of 5 litres at 27◦C. Calculate the pressure using van der Waals’ equation. (a = 4.17 L2 atm mol-2 and b = 0.0371 L mol-1).