Heisenberg’s Uncertainty Principle:
The position and velocity of any moving bodies which we come across in our daily life can be determined accurately at a particular instant of time. However, Heisenberg pointed out that we cannot measure both the position and velocity (momentum) simultaneously with absolute accuracy of microscopic particles. e.g. electron.
Therefore, according to Heisenberg’s uncertainty principle, “It is impossible to know simultaneously both the position and velocity (momentum) of a microscopic particle with absolute accuracy or certainty”. Mathematically, Heisenberg’s uncertainty principle can be written as follows-
∆x.∆p = h/4π
Where,
∆x = uncertainty in position of the particle.
∆p = uncertainty in momentum of the particle.
The sign ≥ means, the products ∆x and ∆p can either be greater than or equal to h/4π, but can never be less than h/4π. The sign equality refers to minimum uncertainty in the product of ∆x and ∆p and is equal to h/4π. Since, the minimum product of ∆x and ∆p is constant. It means that-
1) If ∆x is small, the position of the particle is measured more accurately, ∆p would be large.
2) On the other hand, if ∆p is small, the momentum of the particle is measured more accurately but ∆x would be large i.e. maximum uncertainty in position.
Further,
∆p = m ∆v
Where, ∆v = uncertainty in velocity of the particle.
Thus, the above relation becomes,
∆x.m∆v = h/4π
Physical concept of Uncertainty Principle:
In order to understand the physical picture of uncertainty principle, let us consider as to how the position of a material object is determined. In order to determine the position of an object, light of suitable wavelength is made to fall on the objects which reflect light. When reflected light is enters our eyes, we see the objects. If the objects is of measurable size, its position and momentum will not change by the impact of the light radiations. Thus, it is possible to know the exact position and momentum. Whereas in the case of sub-microscopic object like electron, the impact of the striking photon causes a large displacement from its normal path. As a result of which both the momentum and position of electron change and sends the electron in a new unpredicted path. Therefore, it is very difficult to measure the exact momentum and position of sub-microscopic particles.
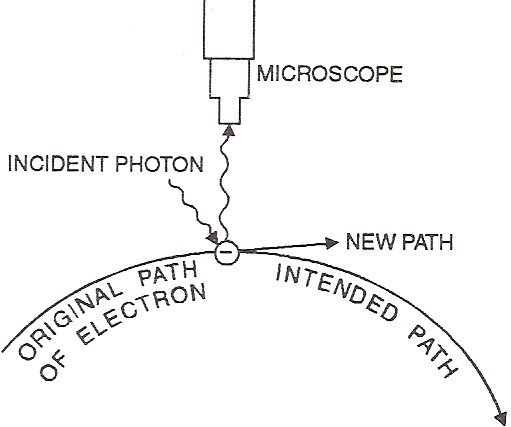
Let us consider a hypothetical experiment to find the position of an electron by using radiation of wavelength λ. The position of an electron changes by the impact of photon of the incident radiation. According to the principle of optics the position of an electron can not be measured more accurately than ± λ. Thus, shorter the wavelength, greater is the accuracy.Therefore, to observe the position of the electron more accurately, radiation of smaller wavelength should be used. But the photon of smaller wavelength will have higher momentum (p =h/ λ). When the photon of such radiation strike against the electron, a large amount of momentum will be transferred to the electron at the time of collision. This will change the momentum of the electron and thus greater uncertainty in momentum (or velocity).
On the other hand, a radiation of smaller momentum is used in order to minimize the change of momentum; it will have a larger wavelength and therefore, position of the electron will be uncertain. Thus, it is not possible to measure simultaneously the position and momentum of small moving objects like electron accurately.