Hess’s Law of Constant Heat Summation:
In 1840 a Russian chemist G.H. Hess proposed an important generalisation regarding the enthalpies (heats) of reactions known as Hess’s law. According to this law- “the enthalpy change (or heat evolved or absorbed) in a particular reaction is the same whether the reaction takes place in one step or in a number of steps.
This means that the amount of heat evolved or absorbed in a chemical reaction depends only upon the enthalpy of initial reactants and the final products irrespective of the path or the manner by which the change has taken place. Suppose in a reaction, the reactant A changes to products B in one step and the enthalpy change during this process is ∆H. Now suppose the same process is carried out in two steps (Fig.1).
i) The reactant A changes to C (intermediate stage) and the enthalpy change during this step is ∆H1.
ii) C changes to the product B and the enthalpy change during this step is ∆H2.
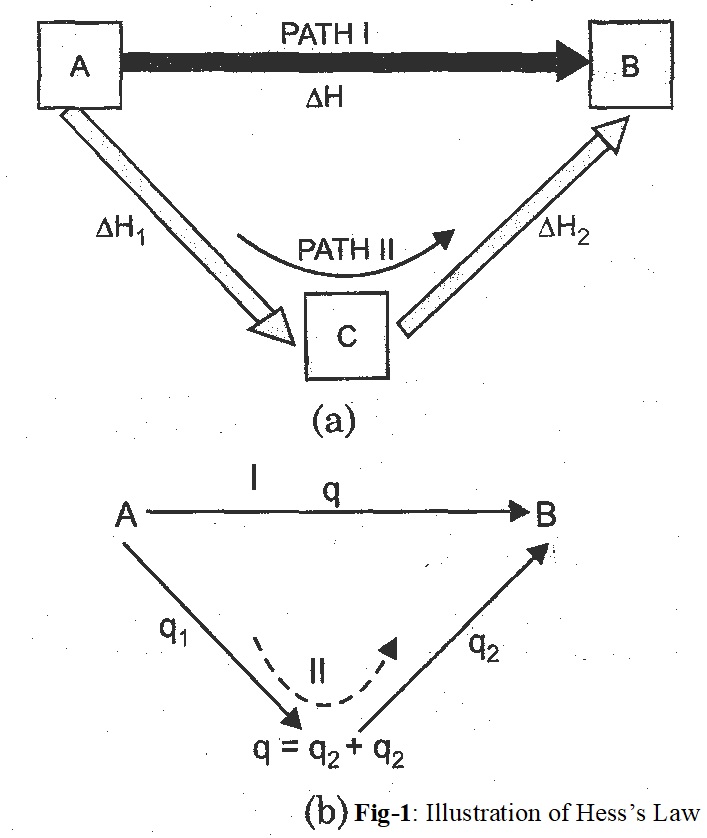
Thus, according to Hess’s law, the enthalpy change for the reaction, whether the reaction follows path I or path II is-
∆H = ∆H1+ ∆H2
Let us illustrate the law by considering the formation of carbon dioxide from carbon and oxygen. Carbon can be converted into CO2 by two ways:
Path-1: C (s) + O2 (g) ——→ CO2 (g) ∆Hf = – 393.5 kJ
Path-2: C (s) + 1/2O2 (g) ——→ CO (g) ∆Hf = – 110.5 kJ
CO (g) + 1/2O2 (g) ——→ CO2 (g) ∆Hf = – 283.0 kJ.
——————————————————————————————
C (s) + O2 (g) ——→ CO2 (g) ∆Hf = – 393.5 kJ
Therefore, ∆H = ∆H1+ ∆H2
Applications of Hess’s Law:
Hess’s law has been found to be very useful in determining the enthalpy changes for the chemical reactions which are not suitable for direct measurements with calorimeter. Therefore, it has many applications in the study of chemical energetics. Some of the important applications of Hess’s law are:
1) Determination of enthalpy of formation of substances which cannot be measured experimentally.
For example, enthalpy of formation of carbon monoxide can be calculated from the enthalpy of combustion data for carbon and carbon monoxide.
i) C (s) + O2 (g) ——→ CO2 (g) ∆Hf = – 393.5 kJ.
ii) CO (g) + 1/2O2 (g) ——→ CO2 (g) ∆Hf = – 283.0 kJ.
By subtracting equation (ii) from equation (i), we get
C (s) + 1/2O2 (g) ——→ CO (g) ∆Hf = – 110.5 kJ.
Thus, the enthalpy of formation of carbon monoxide is -110.5 kJ which has been obtained indirectly from the experimentally determined enthalpy of combustion values of C(s) and CO(g).
2) Determination of enthalpy of transition.
For example, the enthalpies of combustion of diamond and graphite have been found to be -395.4 kJ and -393.5 kJ respectively. The enthalpy of transition of allotropic transformation from diamond to graphite can be calculated with the help of Hess’s law.
The enthalpies of combustion can be represented as:
i) C (diamond) + O2 (g) ——→ CO2 (g) ∆Hf = – 395.4 kJ
ii) C (graphite) + O2 (g) ——→ CO2 (g) ∆Hf = – 393.5 kJ
The conversion can be written as:
C (diamond) ——→ C (graphite) ∆Hf = ?
This can be obtained by subtracting equation (ii) from equation (i)
C (diamond) + O2 (g) ——→ CO2 (g) ∆Hf = – 395.4 kJ.
C (graphite) + O2 (g) ——→ CO2 (g) ∆Hf = – 393.5 kJ.
———————————————————————————————————–
C (diamond) ——→ C (graphite); ∆Hf = – 1.9 kJ
3) Calculation of enthalpy of hydration.
Hess’s law is also useful in calculating the enthalpies of hydration of substances. The enthalpy of hydration is defined as the enthalpy change (heat evolved or absorbed) when one mole of the anhydrous salt combines with the required number of moles of water to form hydrated salt. For example, the enthalpy of hydration of copper sulphate is -78.2 kJ. This may be represented as:
CuSO4(s) + 5H2O ——→ CuSO4. 5H2O (s) ∆Hf = – 78.2 kJ
This can be calculated from the enthalpies of solution of anhydrous and hydrated salts as illustrated below:
Question:-The enthalpies of solution of anhydrous CuSO4 and hydrated CuSO4. 5H2O are -66.5 and 11.7 kJ mol-1 respectively. Calculate the enthalpy of hydration of CuSO4 to CuSO4. 5H2O.
Solution. The required equation is:
CuSO4(s) + 5H2O (l) ——→ CuSO4. 5H2O (s) ∆fH =? kJ
Given that
CuSO4(s) + aq ——→ CuSO4 (aq) ∆fH1 = – 66.5 kJ
CuSO4. 5H2O (s) + aq ——→ CuSO4 (aq) ∆fH2 = + 11.7 kJ
∆fH1 = ∆fH + ∆fH2
∆fH = ∆fH1 – ∆fH2
∆fH = -66.5 – 11.7 = -78.2 kJ.
4) Predicting enthalpies of various reactions
Hess’s law is useful to calculate enthalpies of many reactions whose direct measurement would be difficult or even quite impossible.