Molecular Orbital Theory (MOB):
Molecular orbital theory is modern and more rational. This theory assumes that in molecules, atomic orbitals lose their identity and the electrons in molecules are present in new orbitals called molecular orbital. This molecular orbital are not associated with a particular atom but belongs to molecules as a whole. A brief outline of this theory is given below:
i) In a molecule, electrons are present in new orbitals called molecular orbitals. Molecular orbitals just like atomic orbitals are characterized by a set of quantum numbers.
ii) Molecular orbitals are formed by combination of atomic orbitals of equal energies (incase of homonuclear molecules) or comparable energies.
iii)The number of molecular orbitals formed is equal to the number of atomic orbitals undergoing combination.
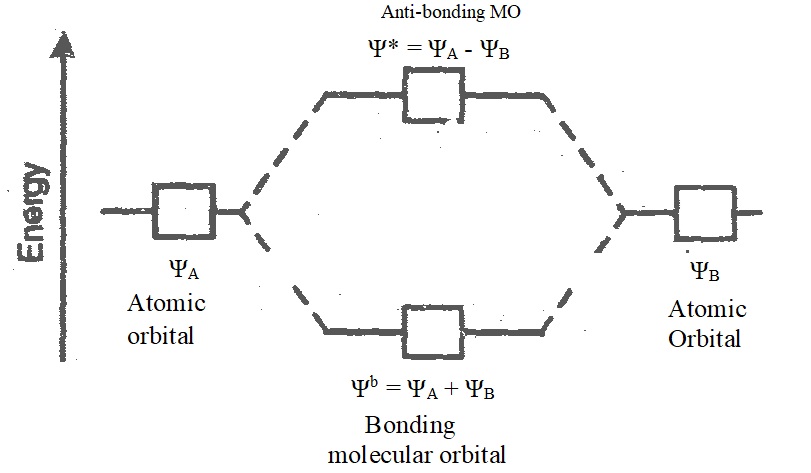
iv)Two atomic orbitals can combine to form two molecular orbitals. One of these two molecular orbitals has a lower energy and the other has a higher energy than either of the combining atomic atomic orbitals. The molecular orbital with lower energy is called bonding molecular orbitals and the other with higher energy is called anti-bonding molecular orbitals.
v) The shape of molecular orbitals depends upon the shape of atomic orbitals.
vi) The bonding molecular orbitals are represented by Greeks letter σ (sigma), π (pi), δ (delta) and the anti-bonding molecular orbitals are represented by σ* (sigma), π* (pi), δ* (delta) respectively.
Formation of Molecular Orbitals (Linear combination of atomic orbitals, LCAO):
Molecular orbitals are formed by the combination of atomic orbitals of bonded atoms. In wave mechanics, each electron is describe by a wave function Ψ. These wave functions are obtained from Schrödinger’s wave equation. In case of atomic orbitals, Schrödinger’s wave equation can be written to describe the behavior of electron in molecules. The complete solution of wave equation for an atom with many electrons is difficult and it is much more difficult for a molecule with two or more nuclei. Therefore, some simplification is required. The approach commonly used is the LCAO approximation.
Linear combination means the simple addition or substruction of wave functions of a given number of atomic orbitals to the same number of molecular orbital wave functions. Suppose, there are two atoms, A and B with atomic wave functions ΨA and ΨB. If the electron is near the atom A, then the atomic orbital wave function ΨA gives a good description of the electron in the molecules. Similarly, atomic orbital wave function ΨB gives a good description of the electron near to the atom B. Then, a linear combination of ΨA and ΨB will be better wave function for the molecule.
For homonuclear diatomic molecules such as hydrogen molecule (H2), let us consider the two atoms of hydrogen in the hydrogen molecule as A and B. Each hydrogen atom contains one electron in 1s-orbital in ground state. These atomic orbital may be represented by the wave function ΨA and ΨB. In this case, the linear combination of ΨA and ΨB are shown below:
ΦMO = ΨA ± ΨB
Ψb = ΨA + ΨB
Ψ* = ΨA – ΨB
Where, Ψb = Bonding molecular orbital
Ψ* = Anti-bonding molecular orbital
ΨA = Wave function of atom A.
ΨB = Wave function of atom B.
The molecular orbital formed by addition of atomic orbitals is called bonding molecular orbitals and the molecular orbital formed by substruction of atomic orbitals is called anti-bonding molecular orbital.
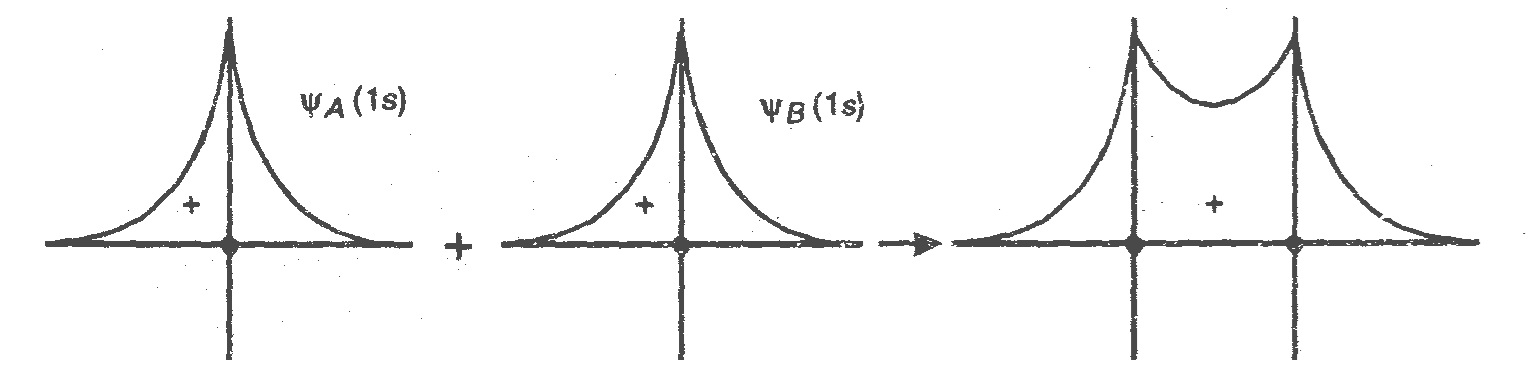Fig: The radial Part of the atomic and molecular wave functions when the wave functions are of the same sign.
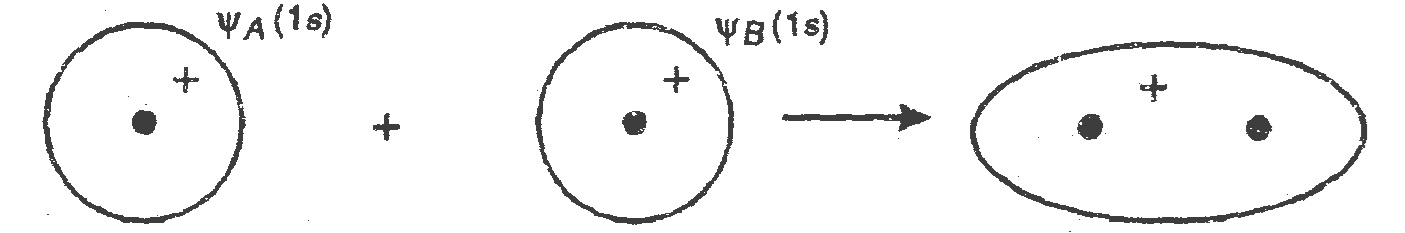
Atomic Orbitals (1s) σ1s (Bonding molecular orbital)
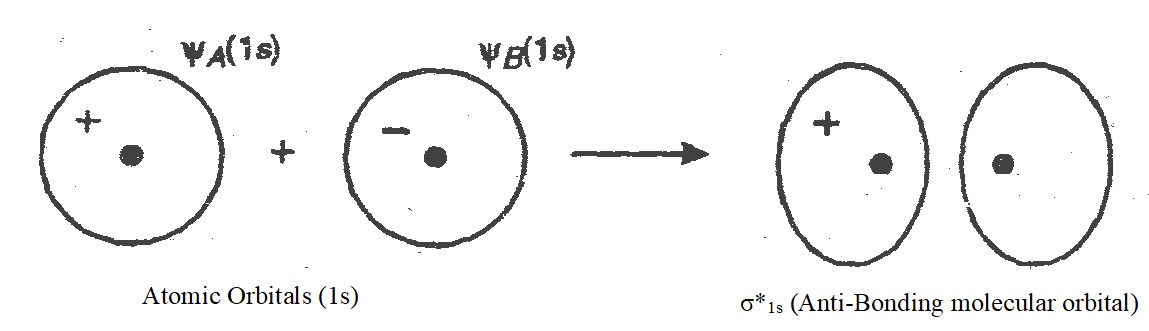
Conditions For The Combination Of Atomic Orbitals:
Only those atomic orbitals can combine to form molecular orbitals which full-filled the following conditions—
- The combining atomic orbitals should have comparable energies.
- The extent of overlap between the atomic orbitals should be large.
- The atomic orbitals must have proper orientations.
Sigma Molecular Orbital:
The molecular orbital which are cylindrically symmetrical around the inter-nuclear axis are called σ (sigma) molecular orbitals. For example, the molecular orbital formed by addition of two 1s-atomic orbitals is designated as σ1s and the molecular orbital formed by substruction of two 1s-atomic orbitals is designated as σ*1s. Similarly, σ2s and σ*2s.
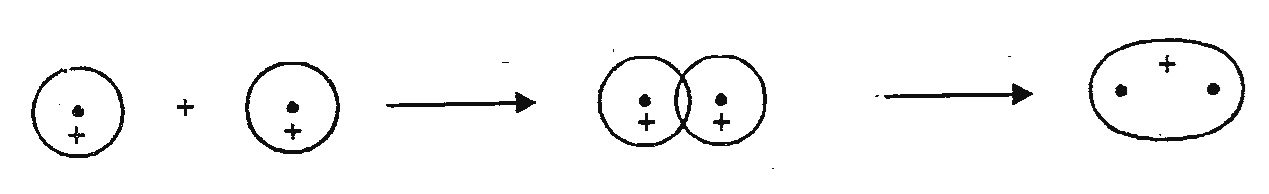1s 1s overlapping σ1s (Bonding molecular orbital)
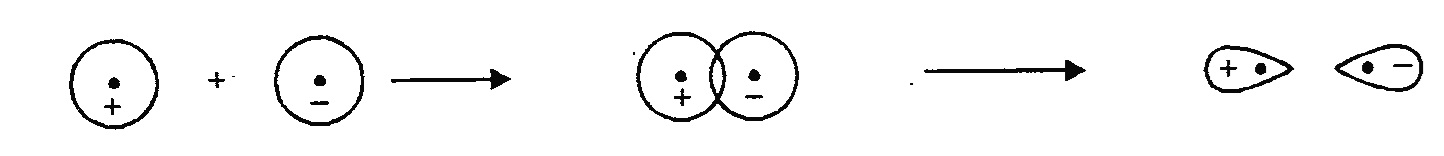1s 1s overlapping σ*1s (Anti-Bonding M-orbital)
Among 2p atomic orbitals, the molecular orbital formed by addition overlap of two 2pz atomic orbitals is designated as σ2pz and the molecular orbital formed by substruction overlap of two 2pz atomic orbitals is designated σ*2pz.
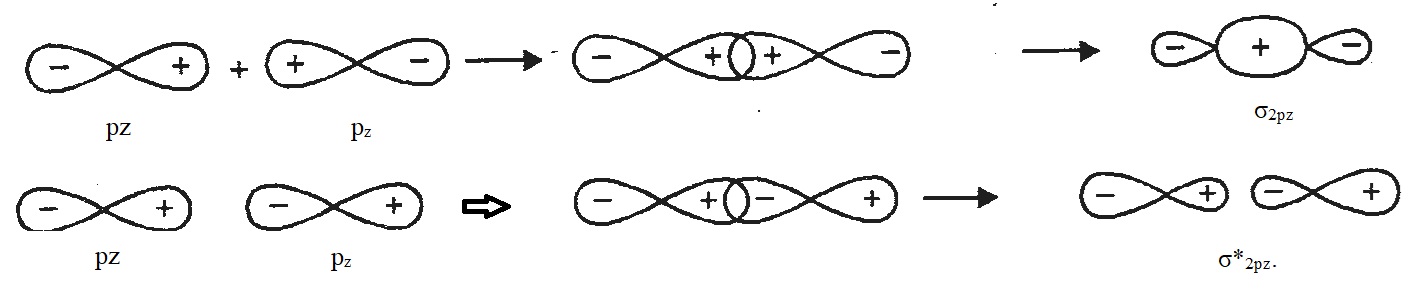Pi (π) Molecular orbital:
The molecular orbitals which are formed by lateral (sidewise) overlap of p-orbitals are called π-molecular orbitals. E.g. addition and substruction overlap of two 2px-atomic orbitals result in the formation of π2px and π*2px molecular orbitals.
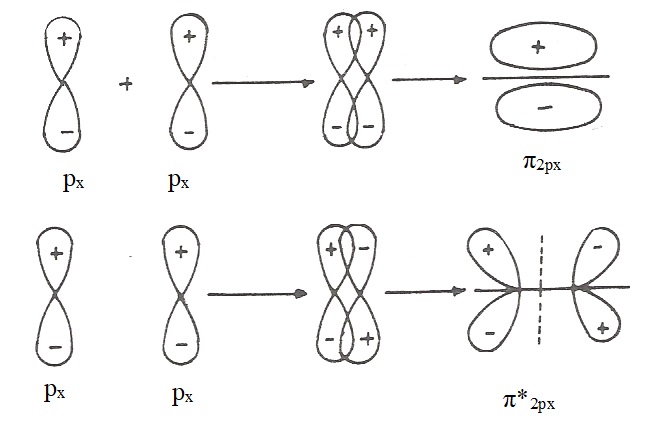Similarly, addition and substruction overlap of two 2py-atomic orbitals result in the formation of π2py and π*2py molecular orbitals.
Energy Level Diagram For Molecular Orbitals:
In case of homonuclear diatomic molecules, combining of two 1s-atomic orbitals of participating atom give rise to two new molecular orbitals designated as σ1s and σ*1s. Similarly, when 2s and three 2p orbitals of each atom give rise to new eight molecular orbitals viz. σ2s, σ*2s, π2px, π*2px, π2py,π*2py, σ2pz, σ*2pz (taking Z-axis to be internuclear axis).
Energy levels of these molecular orbitals have been determined experimentally by spectroscopic studies. The order of increasing energy in case of diatomic molecules of first and second period elements of the periodic table is shown below:
σ1s <σ*1s< σ2s<σ*2s, <π2px= π2py< σ2pz <π*2px =π*2py <σ*2pz
However, experimental evidence of oxygen and heavier diatomic molecules has shown that above sequence of energy levels of molecular orbitals is not correct. In case of these elements, the order of energy levels of σ2pz and π2px, π2py is reversed i.e. σ2pz has lower energy than π2pxor π2py. Therefore, the order of increasing energy of molecular orbitals for these molecules is as follows
σ1s <σ*1s< σ2s<σ*2s, < σ2pz <π2px= π2py <π*2px =π*2py <σ*2pz
Note: This order of energies of various MOs is valid for molecules or ions like O2, O2–(super oxide), O2-2(peroxide), F2, and Ne2 (hypothetical).
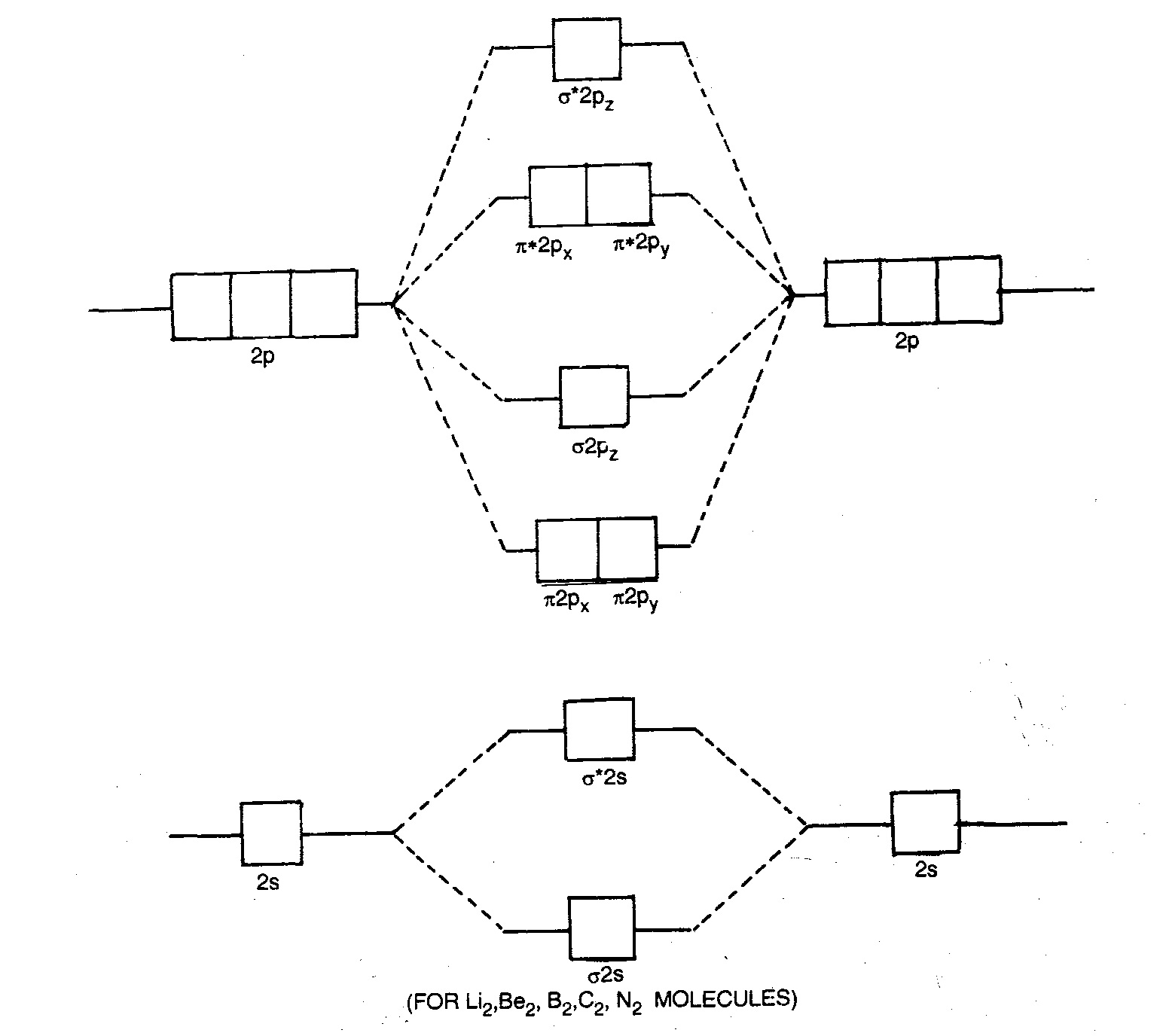Fig: Molecular orbital diagram for diatomic molecules of first and second period (except O2, F2, Ne2 etc) elements.
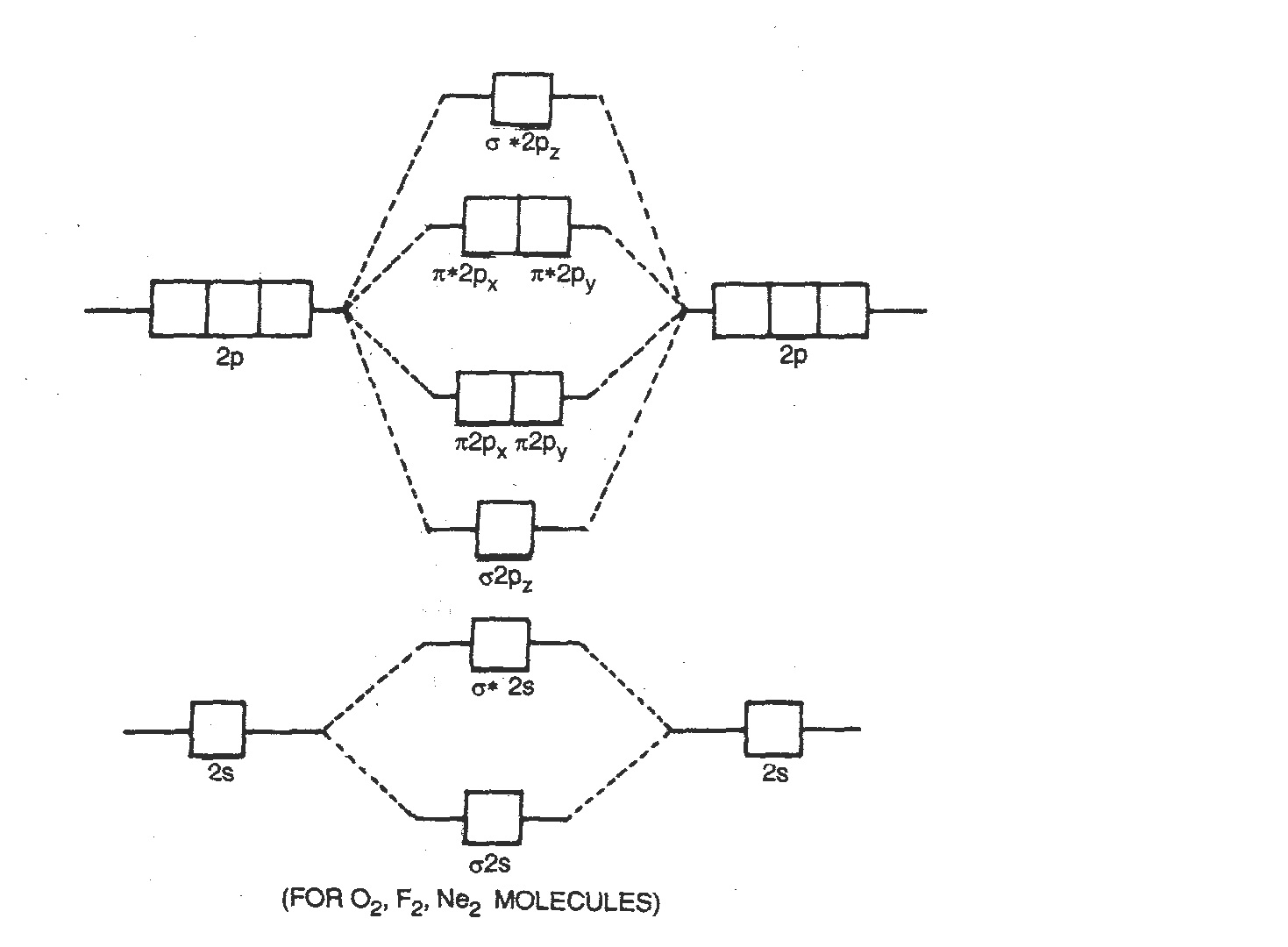Fig: Molecular orbital diagram for diatomic molecules of O2, F2, Ne2 etc. elements.