Shape of Atomic orbitals

Shape of orbitals:

An orbital is the region of space around the nucleus within which the probability of finding electron of a given energy is maximum. The shape of this region (electron cloud) gives the shape of the orbitals. Let us consider the individual shapes-

Shape of s-orbital:

For s-orbital, when l=0, the value of m is zero i.e. there is only one possible orientation. This means that the probability of finding electron is the same in all direction at a given distance from the nucleus. It should be spherical in shape because a sphere can be defined completely by a single value i.e. its radius. Hence, all s-orbital are non-directional and spherically symmetrical about the nucleus.

The size of an s-orbital depends upon the value of principal quantum number (n); greater the value of ‘n’ larger is the size of the orbital. Therefore, 2s-orbital is larger than 1s-orbital, but both of them are non-directional and spherically symmetrical shape.

An important features of the 2s-orbital is that there is a spherical shell within this orbital where the probability of finding electron is zero. This is called Node or Nodal surface.

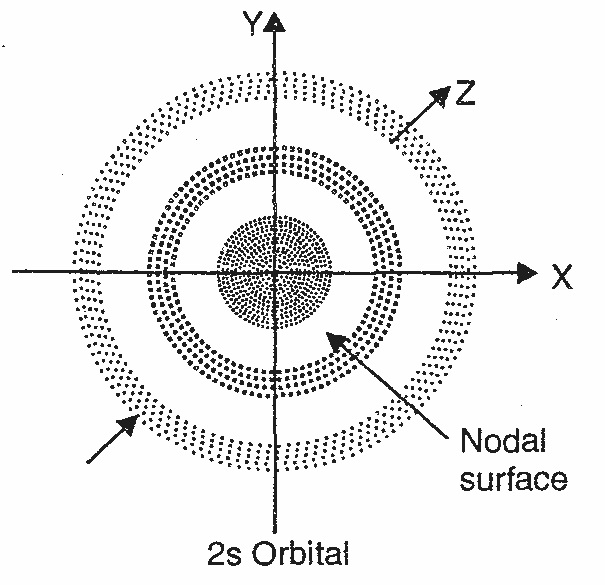
                                                         Fig: Shape of s- orbital

Shape of p-orbital:

For p-subshell, l=1, there are three values of m viz. -1, 0, +1. It means p-orbital can have three possible orientations. These are equal in energy (degenerate state) but differ in their orientations. Each p-orbital consist of two lobes symmetrical about a particular axis. Depending upon the orientation of the lobes, these are denoted by the symbol p_x, p_y and p_z accordingly as they are symmetrical about x, y, and z.

The two lobes of each p-orbital are separated by a nodal plane (a plane having zero electron density). Thus, p-orbitals are dumbbell shape and have directional characters. The probability of finding electron is equal in both the lobes.

Notes: The p-orbitals of higher energy level have similar shapes although their shape, sizes are bigger.

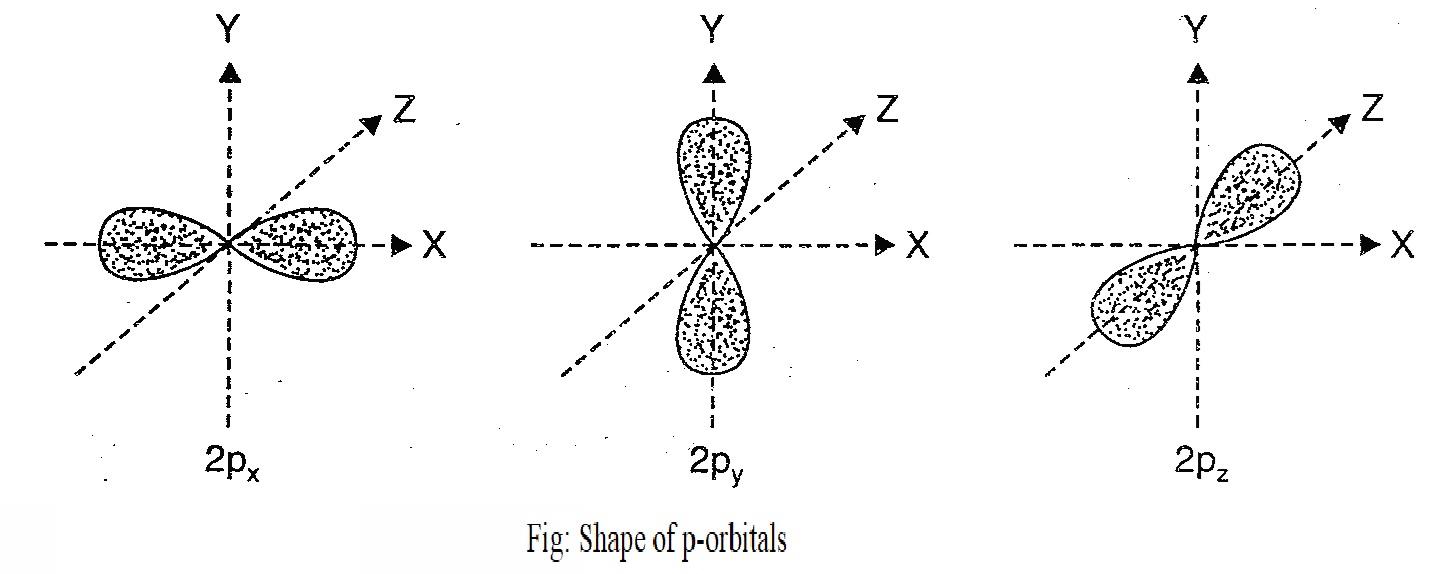Shape of d-orbital:

For d-subshell, l=2, there are five values of m viz. +2, +1, 0, -1, -2. It means d-orbital can have five orientations. These are represented by d_xy, d_xz, d_yz, d_z² and d_x²–_y² respectively. These five orbital are equal in energy (degenerate state), but differ in their orientation. The d_xy, d_xz, and d_yz orbital have same shape but lie in different plane. The d_z² orbital is symmetrical about z-axis and has a dumb-bell shape with doughnut shape electron cloud in the centre. The d_x²–_y² orbital is also clover leaf shaped and lies along x and y axis.

                                                        Fig: Shape of d-orbital.