Integrated rate equation for zero order reaction:
A reaction is said to be of zero order, if its rate is independent of the concentration of the reactants. Consider the general zero order reaction:
A ———-> Product
Let [A] be the concentration of the reactant A and k is the rate constant for the zero order reactions. For the zero order reaction, the rate of reaction is independent of the concentration of A. Then,
– d[A] / dt = k [A]° = k
Rearranging the above equation,
– d[A] = k dt
Integrating the above equation, we get
– ʃd[A] = k ʃdt
– [A] = kt + I —————— (1)
Where, I = integration constant.
If t = 0, then [A] = [A]o. Therefore above equation becomes
– [A]o = k x 0 + I
– [A]o = I
Substituting the value of I in expression (1), we get
— [A] = kt – [A]o
Or, kt = [A]o — [A]
Above equation is called Integrated rate equation of zero order reaction Where [A]o is the initial concentration of A. [A] is the concentration at time t.
Note: The above expression is a straight line equation, thus the value of k can be calculated graphically. On plotting a graph of [A] against t, we get a straight line and the slope of the line is given as Slope= – k
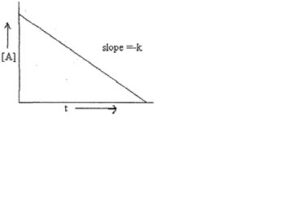
Fig: A plot of [A] against time (t).
Integrated rate equation for first order reaction:
Let us consider a general reaction of first order as-
A ———> Product
If the initial concentration of A is [A]o, k is the rate constant and [A] is concentration at time t, then the differential form of first order reaction can be written as-
– d [A] / dt = k [A]
Rearranging the above equation, we have
– d[A]/ [A]= k dt
Integrating the above equation, we get
Or, – In [A] = kt + I ——————– (2)
Where, I = integration constant.
If t = 0, then [A] = [A]o. Therefore above equation becomes
-In [A]o = k x 0 + I
Or, -In [A]o = I
Substituting the value of I in expression (2), we get
-In [A] = kt – In [A]o
Or, kt = In [A]o – In [A]
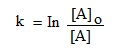
Changing it to common log, we get
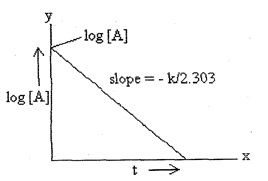
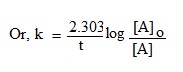Note: The value of k also be calculated graphically by plotting log [A] against time (t) as –
